In the world of statistics, two basic concepts play an important part in understanding the behavior in physical systems. macrostate and microstate. These terms are the basis of fundamental ideas regarding the representation and modeling of energy and matter at the macro and microscopic scales.
A microstate is the most specific, personal description of a system, giving a microscopic overview of its components, which includes the locations and moments of every particle. In contrast, macrostates are an entire system that is based on visible macroscale properties like temperatures, pressures, or energy.
What is Microstate?
Microstate refers to a certain arrangement or configuration of the individual elements or particles in an entire system. It provides a comprehensive and complete explanation of the system on a microscopic level, with a focus on the actions of the individual components.
The position, velocity, and levels of energy for every component are precisely defined at a certain point in time. It covers the precise configuration and characteristics of all elements in the system. For instance, in a gas system microstates are the exact positions and speeds of each gas molecule.
Microstates are typically defined by their extreme degree of detail, taking into account the specific characteristics and interactions of the components. They provide a microscopic view that focuses on the properties and behaviors of each particle or element in the system.
Microstates can be represented as elements in the system’s phase space which is a multidimensional area where every coordinate is associated with the specific properties of the particles or component. Through the consideration of every possible microstate statistical mechanics can allow the computation of macroscopic properties and an analysis of probabilistic behaviors in the system.
Understanding microstates is essential to understanding the fundamental behavior of systems and understanding how macroscopic characteristics emerge through the interaction of the individual components. It serves as a basis for the statistical interpretation of equilibrium states, as well as the investigation of complicated phenomena in fields like the thermodynamics field, statistics mechanics, and material science.
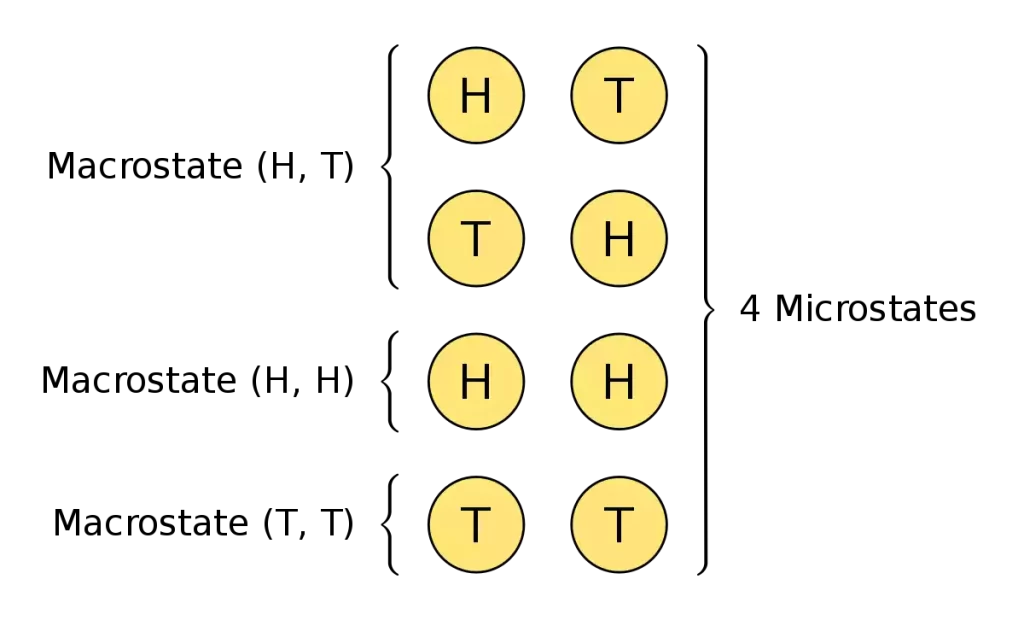
What is Macrostate?
A macrostate describes the general characteristics and properties of a system. They are usually defined in a more general way than the microstate. It concentrates on the general behavior and the observable aspects of the whole system and not the particular characteristics of the individual components.
The primary features of a macrostate are: A macrostate that is observable is a term used to describe measurable variables such as temperature and pressure and volume, energy as well as other macro-scale variables that reflect the state of the system.
Coarse-grained description: Unlike microstates, macrostates are not able to record the exact configuration or characteristics of each particle. Instead, they offer an overall overview of the entire system.
Description of a statistical system: Macrostates often involve statistical averages or probabilistic distributions of microstates that may be in line with the macroscopically defined characteristics. This method of analysis allows for the analysis of large-scale systems and also simplifies the analysis.
A system-level perspective: The macrostates focus on the overall behavior and the emergent characteristics in the systems. They are a good basis for understanding collective phenomena as well as investigating complex systems.
Examples of macrostates are the states of matter (solid liquid gas) and temperatures in equilibrium energies of atoms the general magnetic properties of a substance, and the macroscopic behavior of a species in ecology.
It is vital to understand the fact that one macrostate may be a microstate that reflects different configurations or arrangements of the system, giving the same macroscopic behavior. The relation between microstates and macrostates is an essential notion in the field of statistical mechanics creating a bridge between microscopic and macroscopically oriented descriptions of physical systems.
Microstate and Macrostate in the comparison chart
Here’s a concise comparison chart highlighting the key differences between microstates and macrostates:
| Aspect | Microstate | Macrostate |
|---|---|---|
| Definition | Detailed specification of a system at the microscopic level, including the positions and momenta of individual particles. | Description of a system based on observable, macroscopic properties or averaged properties of an ensemble. |
| Scope of Description | Highly detailed, microscopic view of a single, specific configuration of the system. | Averages over a large number of microstates to provide a simplified, macroscopic view. |
| Variables | Described by specific molecular properties of individual particles. | Described by macroscopic observables, such as temperature, pressure, and energy. |
| Use in Statistical Mechanics | Fundamental for understanding the microcanonical ensemble and the behavior of individual microstates. | Used to characterize the microcanonical ensemble and provide a simplified description of a system in terms of macroscopic properties. |
| Focus | Individual microscopic configurations and their behavior. | Overall, system-level behavior and macroscopic properties. |
| Examples | Specific positions and momenta of gas particles in a container. | The temperature, pressure, and internal energy of the gas in the container. |
| Relationship | Microstates contribute to the properties of macrostates. | Macrostates provide a statistical description of a system based on its microstate distribution. |
This chart summarizes the fundamental distinctions between microstates and macrostates in statistical mechanics, emphasizing the level of detail, variables, and their roles in modeling and understanding physical systems.
Importance of microstate and macrostate
Complex systems described: macrostate and microstate offer complementary ways of describing complex systems. While the microstate reveals the precise behavior of specific parts, the macrostate lets us study the behavior and emergent characteristics of the entire system. Both perspectives are essential for an understanding of the complexity of systems.
Interpretation of statistics: the distinction between macrostate and microstate is the most important aspect of statistical mechanics. It provides an understanding of what happens to large groups of particles. Microstates are individual points within the system’s phase space while macrostates are the result of groups of microstates. Interpretations of statistics, like Boltzmann’s stats or the idea of entropy, depend on this difference to describe uncertain behavior and the equilibrium state of systems.
Predictive ability: macrostate variables, like pressure or temperature can be measured more easily and have a higher degree of predictability than microstate variables. The ability to define and predict the macroscopic behavior of a system, based on its macrostate properties is vital in engineering design and decision-making procedures.
Emergent phenomena: Understanding the connection between macrostate and microstate is crucial to explain emergent phenomena. Complex system-level behaviors result from interactions and the collective effect of the individual components. Examples include phase transitions self-organization and critical phenomena, which can’t be understood fully only by looking at microstates.
Applications that cross disciplines: the concepts of macrostate and microstate have applications across a variety of scientific disciplines. Alongside thermodynamics and statically based mechanics, they also have a place in fields like biology, chemistry, physics as well as computer science and engineering. Knowing the difference allows the use of statistical methods as well as modeling techniques and system-level analysis in these diverse research areas.
Significance and applications
Thermodynamics and statistical mechanics: Concepts of macrostates and microstates are essential to thermodynamics as well as statistical mechanics. They are a way of explaining and analyzing the behavior of systems at the macro and microscopic levels. Statistics mechanics, particularly uses the concept of macrostates and microstates to describe the thermodynamic properties such as phase transitions, phase transitions, and equilibrium state of systems.
Chemical and physical systems: The distinction between macrostate and microstate macrostate is vital to understanding the physical as well as chemical system. It permits the study of various phenomena, including chemical reactions, diffusion phase transitions, and the behavior of gases solids, liquids, and gases. When considering the microstate as well as its statistical interpretation within the context of the macrostate, experts can gain insight into the macroscopic properties and behavior in this system.
The biology of complex systems: Microstate and macrostate also apply to biological systems as well as in studies of complicated systems. In biology understanding the microstate of biomolecules, like nucleic acids and proteins can help to understand their structure-function relations and their dynamic. Descriptions of macrostates, like the dynamics of populations or ecological interactions are essential to understand complicated biological systems at the scale of the ecosystem or organism.
Material science and engineering: The distinction between macrostate and microstate has applications in engineering and materials science. Understanding the microstate of atoms and molecules in a substance allows the creation and development of materials that have specific characteristics. Descriptions of macrostates, like thermal conductivity, and mechanical properties are vital to engineering applications and enhancing the performance of materials.
Applications across disciplines: Understanding macrostate and microstate is important in a wide range of disciplines of science, which allows for cross-disciplinary applications. Researchers can use concepts and techniques from different fields which encourages collaboration and progress in areas like nanotechnology, biophysics and systems biology, and computational sciences.
Conclusion
Understanding the distinction between macrostate and microstate is essential to understanding the behavior of complex systems in a variety of disciplines in science. The microstate is focused on the microscopic scale that provides precise information on specific particles or components of an entire system.
The macrostate, on the other hand, is concerned with the macro level that includes observable properties as well as average values for the entire system.
